martes, 10 de noviembre de 2015

Campo electrodinamico

Campo electrodinámico (movimiento uniforme)[editar]

El campo eléctrico creado por una carga puntual presenta isotropía espacial, en cambio, el campo creado por una carga en movimiento tiene un campo más intenso en el plano perpendicular a la velocidad de acuerdo a las predicciones de la teoría de la relatividad. Esto sucede porque para un observador en reposo respecto a una carga que se mueve con velocidad uniforme la distancia en la dirección del movimiento de la carga serán menores que las medidas por un observador en reposo respecto a la carga, por efecto de la contracción de Lorentz, suponiendo que la carga se mueve a lo largo del eje X de observador tendríamos la siguiente relación de coordenadas entre lo medido por el observador en movimiento respecto a la carga \scriptstyle (\bar{x},\bar{y},\bar{z}) y el observador en reposo respecto a la carga \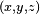scriptstyle (x, y, z):
\bar{x} = \frac{x- Vt}{\sqrt{1-\frac{V^2}{c^2}}}, \quad \bar{y} = y, \quad \bar{z}=z
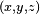Siendo V la velocidad de la carga respecto al observador, así la distancia efectiva a la carga medida por el observador en movimiento respecto a la carga cumplirá que:
\bar{r}^2 = \frac{(x-Vt)^2 + (1-\frac{V^2}{c^2})(y^2+z^2)}{1-\frac{V^2}{c^2}}
Y por tanto el campo eléctrico medido por un observador en movimiento respecto a la carga será:
(19)\bold{E} = \frac{1}{4\pi\epsilon_0} \frac{q}{\|\bar{r}\|^3}\bar{\bold{r}} = \frac{1}{4\pi\epsilon_0} \frac{q\left( 1-\frac{V^2}{c^2} \right)}{r^3\left( 1-\frac{V^2}{c^2}\sin^2 \theta \right)^{3/2}}\bold{r}
Donde \scriptstyle \theta es el ángulo formado por el vector de posición del punto donde se mide el campo (respecto a la carga) y la velocidad del movimiento. De esta última expresión se observa que si se considera una esfera de radio r alrededor de la carga el campo es más intenso en el "ecuador", tomando como polos norte y sur la interasección de la esfera con la trayectoria de la partícula, puede verse que el campo sobre la esfera varía entre un máximo \scriptstyle E_\bot y un mínimo \scriptstyle E_\| dados por:
(20)E_\| =\frac{1}{4\pi\epsilon_0} \frac{q\left( 1-\frac{V^2}{c^2} \right)}{r^2}, \qquad E_\bot = \frac{1}{4\pi\epsilon_0} \frac{q}{r^2\sqrt{ 1-\frac{V^2}{c^2}}}
Esta pérdida de simetría esférica es poco notoria para velocidades pequeñas comparadas con la velocidad de la luz y se hace muy marcada a velocidades cercanas a la luz.
Publicado por en

No hay comentarios:

Publicar un comentario

Suscribirse a: Enviar comentarios (Atom)